
WE Algorithmische Zahlentheorie, Algebraische Geometrie und Kryptologie
Menü
Seminar der WE AlZAGK im WiSe 2012/13
Ikosaeder
Wegen zu geringer Teilnehmeranzahl muss das Seminar dies Semester leider entfallen
(VAK: 03-472)
Ankündigung: (als pdf)
Das Seminar richtet sich an Studierende der Mathematik und Technomathematik ab dem fünften Semester.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| Wegen zu geringer Teilnehmeranzahl muss das Seminar dies Semester leider entfallen. | ||
| 16.10.2012 | J. Gamst, M. Hortmann | Vorbesprechung |
Im kommenden WS wollen wir die Zusammenhänge zwischen Gleichungen 5. Grades, dem Ikosaeder und der alternierenden Gruppe A5 studieren. Das ist ein ganz klassischer Gegenstand und das Thema des „Ikosaederbuchs“ von Felix Klein, eine moderne Darstellung findet sich in:
- J. Shurman:
- „The Geometry of the Quintic“
J. Wiley & Sons 1997
Im Seminar werden nur geringe Vorkenntnisse vorausgesetzt: Algebra und ein wenig komplexe Analysis im Umfang der Standardvorlesungen.
Im letzten Drittel des WS wenden wir uns einer neueren Entwicklung zu, der Lösung von Gleichungen durch Iterationsverfahren nach McMullen. Dazu werden wir uns Einiges aus der Theorie der dynamischen Systeme aneignen müssen.
Literatur:
- F. Klein:
- „Vorlesungen über das Ikosaeder“
Birkhäuser, Teubner 1993 - C. McMullen:
- „Families of rational maps and iterative root-finding algorithms“
in: Annals of Math 125 (1987), S. 467-493 - P. Doyle, C. McMullen:
- „Solving the quintic by iteration“
in: Acta Math 163 (1989), S. 151-180 - J.-P. Serre:
- „Extensions icosaeédriques“
Letter to M. Gray, March 1978
Seminar der WE AlZAGK im SoSe 2012
Moonshine
Di 8:30-10:00 in MZH 7200
(VAK: 03-420)
Ankündigung: (als pdf)
Das Seminar richtet sich an Studierende der Mathematik und Technomathematik ab dem fünften Semester.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| 17.04.2012 | J. Gamst, M. Hortmann | Vorbesprechung |
| 24.04.2012 | P. Pfeiffer | Darstellungstheorie I |
| 01.05.2012 | -- | Tag der Arbeit |
| 08.05.2012 | F. Dreher | Darstellungstheorie II |
| 15.05.2012 | J. Gamst | Darstellungstheorie III |
| 22.05.2012 | J. Gamst | M24 I |
| 29.05.2012 | S. Schlegel | M24 II |
| 05.06.2012 | J. Gamst | M24 III |
| 12.06.2012 | M. Hortmann | Modulformen I |
| 19.06.2012 | J. Nüßle | Modulformen II |
| 26.06.2012 | J. Gamst | Modulformen III |
| 03.07.2012 | A. Libert | Moonshine für M24 I |
| 10.07.2012 | J. Nüßle | Moonshine für M24 II |
| 17.07.2012 | J. Gamst | Moonshine für M24 III |
Ende der siebziger Jahre des vorigen Jahrhunderts wurden bemerkenswerte Koinzidenzen entdeckt, u. a.:
196884 = 196883 + 1
das Produkt der Primteiler von n (ohne Vielfachheiten).
Links steht der Koeffizient von q in der q-Entwicklung der j-Funktion, rechts steht 1 + Dimension der kleinsten nichttrivialen irreduziblen Darstellung der Monstergruppe (der größten unter den 26 sporadischen einfachen endlichen Gruppen). Spekulationen hierüber liefen unter dem Namen „moonshine“. Inzwischen ist einiges bewiesen, insbesondere durch R. E. Borcherds 1998.
Eine einfachere Version dieser Zusammenhänge hat man nach G. Mason 1985 für eine andere der sporadischen einfachen Gruppen, die MathieuGruppe M24 der Ordnung
#M24 = 210 ⋅ 33 ⋅ 5 ⋅ 7 ⋅ 11 ⋅ 23 = 244823040
Dazu gibt es die AB Thesis (artium baccalaureus) von J. Booher (Harvard, 2010), welche wir dem Seminar zu Grunde legen.
Grobeinteilung der Vortragsthemen:
- Darstellungen endlicher Gruppen (4V)
- Konstruktion der MathieuGruppe M24 (4V)
- Modulformen (3V)
- Moonshine für M24 (3V)
Vorkenntnisse:
Algebra und komplexe Analysis auf dem Niveau der Grundvorlesungen, etwas Computeralgebra (z. B. SAGE).Literatur:
- J. Booher:
- „The spirit of Moonshine. Connections between the Mathieu
Groups and Modular Forms“
Harvard, 2010 - R. Busam, E. Freitag:
- „Funktionentheorie“
Springer, 4. Aufl. 2006 - R. Griess:
- „Twelve Sporadic Groups“
Springer, 1998 - L. J. P. Kilford:
- „Modular Forms“
Imperial College Press, 2008 - S. Schlegel:
- „Computeralgebra und Gruppentheorie“
Diplomarbeit, Universität Bremen, 2012 - J.-P. Serre:
- „Linear Representations of Finite Groups“
Springer, 1977 - J.-P. Serre:
- „A Course in Arithmetic“
Springer, 1996 - R. A. Wilson:
- „The Finite Simple Groups“
Springer, 2009
Seminar der WE AlZAGK im WiSe 2011/2012
Algebraische Dynamische Systeme
Di 8:30-10:00 in MZH 7200
(VAK: 03-472)
Ankündigung: (als pdf)
Das Seminar richtet sich an Studierende der Mathematik und Technomathematik ab dem fünften Semester.
| Termin | Vortragender | Thema des Vortrages | Literatur |
|---|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | |||
| 01.11.2011 | J. Gamst, M. Hortmann | Vorbesprechung | |
| 08.11.2011 | M. Hortmann | Introduktion | |
| 15.11.2011 | Philipp Pfeiffer | Maximale Perioden von Orbits des BBS Generators (Teil 1) | Encinas |
| 22.11.2011 | Philipp Pfeiffer | Maximale Perioden von Orbits des BBS Generators (Teil 2) | Encinas |
| 29.11.2011 | Christopher Schael | BBS Erzeuger | Diaz |
| 06.12.2011 | Marie van Amelsvoort | Maximale Perioden von x2 + c in Fq (Teil 1) | Peinado |
| 13.12.2011 | Stefan Hamcke | Maximale Perioden von x2 + c in Fq (Teil 2) | Peinado |
| 20.12.2011 | Andreas Libert | Arithmetik von dynamischen Systemen | Silverman |
| Weihnachtsferien vom 24. Dezember 2011 bis zum 7. Januar 2012 | |||
| 10.01.2012 | -- | entfällt | |
| 17.01.2012 | Thomas Sievers | Variation eines Irrationalitätsbeweises von Fourier | Waldschmidt, Kap. 1.2 |
| 24.01.2012 | M. Hortmann | Irrationalitätskriterien | Waldschmidt, Kap. 1.3 |
| 31.01.2012 | J. Gamst | Irrationalität von er und π | Waldschmidt, Kap. 1.4 |
| 07.02.2012 | H. Özuguz | ||
Für uns wird ein Dynamisches System zunächst einfach gegeben sein durch eine Abbildung T: M → M einer Menge M in sich, bei der man sich für Fixpunkte oder allgemeiner periodischen Punkte x von T interessiert, d.h mit Tn(x) = x. Unter diesem Gesichtspunkt kann man einige Faktorisierungsverfahren subsumieren.
Bei der Pollardschen „Rho-Methode“ z.B, mit der die Primfaktoren einer Zahl n=pq gefunden werden sollen, hat man M = Z/nZ, und T ist gegeben durch ein Polynom mit ganzen Koeffizienten. Mit einem Startwert x0 bildet man die Folge xi = Ti(α0) und erreicht schließlich einen Zyklus xk, xk+1, xk+l = xk.
Man berechnet daher die ggT(xi-xj, n) und hofft, dass die Periodizität schon mod p oder mod q auftritt, sodass der obige ggT dann ein echter Teiler von n ist. Die ersten Vorträge beziehen sich auf neuere Arbeiten zur Periodenlänge von x → x2+c über Fq oder Z/nZ mit n=pq.
Im weiteren Verlauf des Seminars behandeln wir einen Übersichtsartikel von H. Niederreiter und I. Shparlinski und skizzieren dann einen allgemeinen Rahmen der Theorie nach einem Buch von J. Silverman. Wenn Zeit bleibt, sehen wir uns auch Anwendungen in der diophantischen Analysis nach einem Kurs von M. Waldschmidt an.
Literatur:
- J. H. Silverman (DOI):
- „The Arithmetic of Dynamical Systems“
Springer, Berlin, 2007 - Luis Hernández Encinas (BibTeX):
- „Maximal period of orbits of the BBS generator“
In Proceedings of ICISC, 1998. S. 71-80 - Raúl Durán Díaz, Alberto Peinado Domínguez (pdf):
- „BBS generator using the function x2 − 2 (mod n)
- A. Peinado, F. Montoya, J. Muñoz, A. J. Yuste (DOI):
- „Maximal Periods of x2 + c in Fq“
in: Lecture Notes in Computer Science, 2227, p. 219-228 - Harald Niederreiter, Igor E. Shparlinski (DOI):
- „Dynamical Systems Generated by Rational Functions“
in: Lecture Notes in Computer Science, 2643, p. 606 - Michel Waldschmidt (pdf):
- „Introduction to Diophantine Methods“
Seminar der WE AlZAGK im SoSe 2011
Ein Algorithmus für das Diskrete Logarithmusproblem auf elliptischen Kurven über Erweiterungskörpern endlicher Körper Fq
Di 8:30-10:00 in MZH 7200
(VAK: 03-472)
Ankündigung: (als pdf)
Im Sommersemester 2011 werden wir uns an Hand der Habilitationsschrift von C. Diem: „On arithmetic and the discrete logarithm problem in class groups of curves“ mit einem Algorithmus für das Diskrete Logarithmusproblem auf elliptischen Kurven über Erweiterungskörpern endlicher Körper Fq beschäftigen, der subexponentielle Laufzeit hat.
Das Seminar richtet sich an Studierende der Mathematik und Technomathematik ab dem fünften Semester.
| Termin | Vortragender | Thema des Vortrages | Literatur | |
|---|---|---|---|---|
| 05.04.2011 | J. Gamst, M. Hortmann | Vorbesprechung und Einleitung | ||
| 12.04.2011 | Johannes Nüßle | Diskrete Logarithmen: Überblick | Carl Pomerance: Discrete Logarithms (Talk 2009) (pdf) | |
| 19.04.2011 | Michael Hortmann | Index-Kalkül: Überblick | Claus Diem: What is Index Calculus? (Vortrag 2008) (pdf) | |
| Osterferien vom 26. April bis zum 30. April 2011 | ||||
| 03.05.2011 | Jens Gamst | Index-Kalkül in der Klassengruppe einer Kurve | Kapitel 3.2 | |
| 10.05.2011 | Jens Gamst | Index-Kalkül in der Klassengruppe einer Kurve II | Kapitel 3.2 | |
| 17.05.2011 | Jens Gamst | Überblick über Theoreme | ||
| 24.05.2011 | Henning Schatz | Zerlegungsalgorithmus | Kapitel 3.5.2.1 | |
| Multihomogene Polynome: | ||||
| 31.05.2011 | J. Gamst | Schnitttheorie I | Kapitel 3.5.4.1 | |
| 07.06.2011 | J. Gamst | Schnitttheorie II | Kapitel 3.5.4.1 | |
| 14.06.2011 | J. Gamst | Multigraduierte Resultanten | Kapitel 3.5.4.2 | |
| 21.06.2011 | J. Gamst | Zusammenfassung: Algorithmus für Theorem 4 | Kapitel 3.5.2.2 | |
| Anwendungen der algebraischen Geometrie: | ||||
| 28.06.2011 | Andreas Libert | Weil-Restriktion | Kapitel 3.5.6.1 | |
| 05.07.2011 | J. Gamst | Geometrie der Faktorbasis | Kapitel 3.5.6.3 + 3.5.6.5 | |
| 08.07.2011 |
AlZAGK-Abschluß: Paddeln auf der Wümme Treffen bei der Kanu-Scheune in Lilienthal: ca. 13:30 Uhr; Abfahrt: 14:00 Uhr Ziel: Restaurant Wümmeblick Höftdeich |
|||
| 12.07.2011 | Christian Janson | Bool'sche Funktionen | ||
Der Algorithmus ordnet sich in den allgemeinen Rahmen der „Index-Kalkül-Methode“ ein, wir beginnen daher mit grundsätzlichen Bemerkungen zu dieser Methode und dem Resultat, dass man damit das Diskrete Logarithmusproblem in F*p in subexponentieller Laufzeit lösen kann.
Im weiteren Verlauf des Seminars folgen wir im Wesentlichen dem Abschnitt 3.5 der Schrift von C. Diem. Die dafür nötigen Kenntnisse über elliptische Kurven und aus der Algebraischen Geometrie werden ohne Beweise hingenommen.
Literatur:
- Diem, Claus (pdf):
- „On arithmetic and the discrete logarithm problem in class groups of curves“
Habilitationsschrift an der Universität Leipzig (2008)
Seminar der WE AlZAGK im WiSe 2010/11
Faktorisierung und diskreter Logarithmus
Do 8:30-10:00 in MZH 7200
(VAK: 03-468)
Ankündigung: (als pdf)
Im Wintersemester 2010/11 werden wir uns mit Faktorisierung und dem diskreten Logarithmus beschäftigen.
Das Seminar richtet sich an Studierende der Mathematik und Technomathematik ab dem fünften Semester. Behandelt werden Lösungsansätze für zwei zahlentheoretische Probleme, auf deren Schwierigkeit wichtige kryptographische Protokolle beruhen.
Interessenten/innen können sich vorab in Stud.IP unverbindlich für das Seminar anmelden.
| Termin | Vortragender | Thema des Vortrages | Betreuer | |
|---|---|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||||
| 28.10.2010 | J. Gamst, M. Hortmann | Vorbesprechung und Einleitung | ||
| 04.11.2010 | L. Becker | Fermat-Faktorisierung | M. Hortmann | |
| 11.11.2010 | N. Kemlein | Kettenbrüche | J. Gamst | |
| 18.11.2010 | D. Badem | Faktorisierung mit Kettenbrüchen (CFRAC) | J. Gamst | |
| 25.11.2010 | M. A. van Amelsvoort | Quadratische Formen (Shanks) | M. Hortmann | |
| 02.12.2010 | M. N. Sinning | Glatte Zahlen I | J. Gamst | |
| 09.12.2010 | S. Riedel | Glatte Zahlen II | J. Gamst | |
| 16.12.2010 | C. Plump | Zahlkörpersieb I (NFS) | M. Hortmann | |
| Weihnachtsferien vom 22. Dezember 2010 bis zum 4. Januar 2011 | ||||
| 06.01.2011 | H. Özoguz | Zahlkörpersieb II | M. Hortmann | |
| 13.01.2011 | A. Kankeu | Diskreter Logarithmus, Baby-Step/Giant-Step, Indexkalkül | M. Hortmann | |
| 20.01.2011 | D. Lachmund | Elliptische Kurven I | J. Gamst | |
| 27.01.2011 | I. Beckmann | Elliptische Kurven II (Faktorisierung, (p-1)(p+1)-Methode) | J. Gamst | |
| 03.02.2011 | J. F. Senge & H. Schatz | Diskretes Logarithmusproblem auf Elliptischen Kurven I | ||
| 10.02.2011 | J. F. Senge & H. Schatz | Diskretes Logarithmusproblem auf Elliptischen Kurven II | ||
Seminar der WE AlZAGK im SoSe 2010
Die ABC-Vermutung
Di 8:30-10:00 in MZH 7200
(VAK: 03-404)
Ankündigung: (als pdf)
Im Sommersemester 2010 werden wir uns mit den elementaren und weniger elementaren Aspekten der ABC-Vermutung beschäftigen.
Die vermutete Aussage ist:
Zu jedem ε>0 existiert eine Konstante Kε, so daß für teilerfremde ganze Zahlen a,b,c≠0 mit a+b+c=0 gilt:
max(|a|,|b|,|c|) ≤ Kε rad1+ε (abc).
Dabei ist allgemein für ganze Zahlen n≠0:
rad(n) = ∏p|np
das Produkt der Primteiler von n (ohne Vielfachheiten).Die Vermutung entstand 1985 bei Diskussionen von Masser und Oesterlé anläßlich eines Vortrages im Séminaire Bourbaki über den (damals noch unbewiesenen) „großen Satz von Fermat“. Sie hat weitreichende Konsequenzen in der Diophantischen Geometrie der elliptischen Kurven und abelschen Varietäten, aber es gibt auch eine Fülle elementarer Anwendungen, vgl. den betreffenden Wikipedia-Artikel.
Ein ausfürlicher Vortragsplan inkl. Literaturangaben ist von H. Özoguz ausgearbeitet worden und kann hier geladen werden.
| Termin | Vortragender | Thema des Vortrages | ||
|---|---|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||||
| 06.04.2010 | H. Özoguz | Einleitung | ||
| 13.04.2010 | F. Dreher | Diophantisches in Polynomringen (1) | ||
| 20.04.2010 | P. Niemann | Diophantisches in Polynomringen (2) | ||
| 27.04.2010 | D. Badem | Dichte quadratfreier Polynomwerte (1) | ||
| 04.05.2010 | J. Nüßle | Dichte quadratfreier Polynomwerte (2) | ||
| 11.05.2010 | G. Grenzebach | Vermutung von Brocard + Vermutung von Erdös-Woods | ||
| 18.05.2010 | -- | entfällt | ||
| 25.05.2010 | J. Gamst | Satz von Mordell/Faltings: Einführung | ||
| 01.06.2010 | J. Gamst | Satz von Mordell/Faltings: Weilsche Höhenmaschine & Das Argument von Elkies | ||
| 08.06.2010 | -- | entfällt | ||
| 15.06.2010 | N. Prizigoda | Wieferich-Primzahlen | ||
| 22.06.2010 | T. Schindler | Kongruenzversion der ABC-Vermutung + Vermutung von Hall | ||
| 29.06.2010 | H. Özoguz | Vermutung von Szpiro | ||
| 07.07.2010 |
AlZAGK-Abschluß: Paddeln auf der Wümme Treffen bei der Kanuscheune in Borgfeld: ca. 13:30 Uhr; Abfahrt: 14:00 Uhr Ziel: Restaurant Wümmeblick Höftdeich |
|||
Seminar der WE AlZAGK im WiSe 2009/10
Die Pellsche Gleichung
Do 8:30-10:00 in MZH 7200
(VAK: 03-404)
Ankündigung: (als pdf)
Im Wintersemester 2009/2010 wollen wir uns mit der Pellschen Gleichung beschäftigen. Dazu werden wir das Buch von M. Jacobson und H. C. Williams (s. u.) zugrundelegen (Kapitelangaben beziehen sich auf dieses Buch).
| Termin | Vortragender | Thema des Vortrages | Literatur | |
|---|---|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||||
| 22.10.2009 | -- | Vorbesprechung | ||
| 29.10.2009 | M. van Amelsvoort | Struktur der Lösungsmenge | Kapitel 1.3 | |
| 05.11.2009 | S. Albrecht | Das problema bovinum des Archimedes | AlZAGK-Vortrag von C. Grenzebach (pdf, ps) | |
| 12.11.2009 | J. Fisahn | Die Aufgabe von Fermat | A. Weil „Number Theory: An Approach through History“ | |
| 19.11.2009 | A. El Attur | Kettenbrüche | Kapitel 3 | |
| 26.11.2009 | A. Düvel | Quadratische Zahlkörper: Ordnungen und Einheiten | Kapitel 4.1–4.3 | |
| 03.12.2009 10.12.2009 |
H. Schatz | Quadratische Zahlkörper: Ideale | Kapitel 4.4–4.6 | |
| 17.12.2009 | J. Gamst | Reduktion von Idealen | Kapitel 5.1–5.2 | |
| Weihnachtsferien vom 21. Dezember 2009 bis zum 2. Januar 2010 | ||||
| 07.01.2010 | J. Gamst | Reduktionstheorie I | ||
| 14.01.2010 | J. Gamst | Reduktionstheorie II | ||
| 21.01.2010 | H. Özuguz | BabyStep/GiantStep für die Infrastruktur | Kapitel 8.3–8.5 | |
| 28.1.2010 | T. Jankowski | Dirichlet Charaktere | Kapitel 8.1–8.2 | |
Die Gleichung
T2 − DU2 = 1,
wobei D ∈ N kein Quadrat ist, wurde von L. Euler fälschlich J. Pell zugeschrieben und wird seitdem Pellsche Gleichung genannt. Sie trat allerdings schon in der Antike, bei Archimedes z.B., auf und wurde auch in der Indischen Mathematik des 7. Jahrhunderts erfolgreich behandelt.
Man sucht ganzzahlige Lösungen (T,U) der Gleichung, o.E. nichttrivial, d.h. mit U ≠ 0, und kann sich auf T,U>0 beschränken. Solche Lösungen existieren stets, und ist (t,u) die Lösung mit t+u√D minimal, so gilt für die betrachteten Lösungen (T,U):
T + U√D = (t + u√D)n
mit n>0. Daher heißt (t,u) FundamentalLösung der Pellschen Gleichung.
Die effektive Bestimmung der FundamentalLösung ist allerdings ein Problem: bei D=1621 z.B. ist t eine Zahl mit 76 Dezimalstellen. Hier hat man anfangs mit Kettenbrüchen gearbeitet, bessere Algorithmen gibt es erst seit 20 Jahren (H.W. Lenstra, J. Buchmann et al). Dabei geht einiges über den reellquadratischen Zahlkörper Q(√D) ein.
Diese neueren Ergebnisse werden dargestellt in:
- Michael J. Jacobson, Jr., Hugh C. Williams (DOI):
- „Solving the Pell Equation“
Series: CMS Books in Mathematics
Springer, Berlin, 2009,
ISBN: 978-0-387-84922-5
Seminar der WE AlZAGK im SoSe 2009
Primzahltests
Do 8:30-10:00 in MZH 7200
(VAK: 03-404)
Ankündigung: (als pdf)
Im SS 09 wollen wir verschiedene Primzahltests behandeln.
| Termin | Vortragender | Thema des Vortrages | |
|---|---|---|---|
| 9.04.2009 | -- | Vorbesprechung | |
| A. Nach R. Schoof: „Four primality testing algorithms“ | |||
| 16.04.2009 | M. König | Miller-Rabin Test | Theorem 2.1 |
| 23.04.2009 | C. Hertzberg | Miller-Rabin Test | Theorem 2.2 |
| 30.04.2009 | R. Stein | Agrawal-Kayal-Saxena Test | Theorem 3.1 |
| 07.05.2009 | P. Kirchgessner | Agrawal-Kayal-Saxena Test | Theorem 3.1 |
| 14.05.2009 | N. Przigoda | Laufzeitanalyse und Diskussion | |
| 21.05.2009 | -- | Himmelfahrt | |
| B. Nach J.-M. Couveignes, T. Ezome, R. Lercier: „Elliptic Periods and Primality Proving“ | |||
| 28.05.2009 | M. Dlugosch | Allgemeine Idee | Lemma 1 & 2 |
| 04.06.2009 | J. Gamst | Rechnungen mit Isogenien | Abschnitt 3 |
| 11.06.2009 | J. Gamst | Rechnungen mit Isogenien | Abschnitt 3 |
| 18.06.2009 | G. Grenzebach | Universelle Weierstraßkurven | Theorem 1 |
| 25.06.2009 | R. Donau | Ring der elliptischen Perioden | Theorem 2 |
| 02.07.2009 | H. Özoguz | Primzahltest | Theorem 3 |
| 09.07.2009 | Diskussion | Abschnitt 7 | |
| 01.07.2009 |
AlZAGK-Abschluß: Paddeln auf der Wümme Start: 14:00 Uhr ab der Kanuscheune in Borgfeld Ziel: Restaurant Wümmeblick Höftdeich |
||
Die Verfahren zur Primzahlerkennung sind mittlerweile so weit
entwickelt worden, daß es eine Routineaufgabe ist, bei
Zahlen von einigen tausend Dezimalstellen den Nachweis zu
führen, daß sie Primzahlen sind.
Von besonderem theoretischen Interesse ist dabei das Resultat
einer Gruppe indischer Wissenschaftler
(M. Agrawal, N. Kayal, N. Saxena: „Primes is in P“),
die zum ersten Mal einen Primzahltest vorstellten, dessen
Laufzeit polynomial ist:
Die Behandlung einer Zahl n erfordert eine Laufzeit von höchstens (log n)12+o(1).
Natürlich gibt es inzwischen eine ganze Reihe von Verbesserungen, zuletzt: J.-M. Couveignes, T. Ezome, R. Lercier: „Elliptic Periods and Primality Proving“.
Im SS 09 werden wir uns zunächst orientieren an R. Schoof: „Four primality testing algorithms“ und dann den o. g. Artikel von Couveignes et al. studieren, unter wesentlicher Benutzung von J.-M. Couveignes, R. Lercier: „Elliptic periods for finite fields“.
Literatur:
- M. Agrawal, N. Kayal, N. Saxena (pdf):
- „Primes is in P“
Annals of Mathematics 160 (2004), 781-793 - R. Schoof (pdf):
- „Four primality testing algorithms“
in: Algorithmic Number Theory,
MSRI Publications 44,
Cambridge University Press, Cambridge, 2008, S. 101-126 - S. V. Konyagin, C. Pomerance (pdf):
- „On primes recognizable in deterministic polynomial time“
in: The Mathematics of Paul Erdös I,
R. L. Graham and J. Nešetřil, eds.
Algorithms and Combinatorics 13,
Springer, Berlin, 1997, S. 176-198 - E. Bach (pdf):
- „Explicit Bounds for Primality Testing and Related Problems“
Mathematics of Computation, Vol. 55, No. 191 (1990), 355-380 - J.-M. Couveignes, T. Ezome, R. Lercier (pdf):
- „Elliptic Periods and Primality Proving“
arXiv: 0810.2853 - J.-M. Couveignes, R. Lercier (DOI):
- „Elliptic periods for finite fields“
Finite Fields and Their Applications 15 (2009), 1-22 - J. Vélu (pdf):
- „Courbes elliptiques munies d'un sous-groupe Z/nZ × μn“
Mémoires de la Société Mathématique de France 57 (1978), 1-152
Seminar der WE AlZAGK im WiSe 2008/09
Die Catalansche Vermutung
Do 8:30-10:00 in MZH 7200
(VAK: 03-404)
Ankündigung (als pdf):
Im WS 08/09 wollen wir an Hand eines neuen Buches von R. Schoof (s. u.) die Catalansche Vermutung behandeln.
| Termin | Vortragender | Thema des Vortrages | Literatur |
|---|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | |||
| 23.10.2008 | -- | Vorbesprechung | |
| 30.10.2008 | F. Kaufhold |
Levi ben Gershon, q = 2 (Lebesgue) |
R. Schoof (Kapitel 2) |
| 06.11.2008 | E. Bonacker | p = 2 (Chao) | R. Schoof (Kapitel 3) |
| 13.11.2008 | A. Scholz | x2 = y3 + 1 (McCallum) | R. Schoof (Kapitel 4) |
| 20.11.2008 | W. Vogelsang | Cassels I | R. Schoof (Kapitel 6) |
| 27.11.2008 | A. Oster | Cassels II | R. Schoof (Kapitel 6) |
| 04.12.2008 | E. Oeljeklaus | Algebraische Zahlkörper | |
| 11.12.2008 | J. Gamst | Eine HindernisGruppe | R. Schoof (Kapitel 7) und L. Washington |
| 18.12.2008 | C. Kapitza | Doppelter Wieferich | R. Schoof (Kapitel 10) |
| Weihnachtsferien vom 22. Dezember 2008 bis zum 2. Januar 2009 | |||
| 08.01.2009 | J. Gamst | Das Stickelberger Ideal | R. Schoof (Kapitel 9) und L. Washington |
| 15.01.2009 | P. Niemann | Kleine p oder q | R. Schoof (Kapitel 8) |
| 22.01.2009 | H. Özoguz | Das Minus Argument | R. Schoof (Kapitel 11) |
| 29.01.2009 | J. Gamst | Das Plus Argument I | R. Schoof (Kapitel 12) |
| 05.02.2009 | E. Oeljeklaus | Das Plus Argument II | R. Schoof (Kapitel 13, 14) |
Die Vermutung besagt, daß 8 und 9 ein ganz besonders Zahlenpaar bilden: 9 = 32 und 8 = 23 mit 9 − 8 = 1 ist die einzige Lösung in natürlichen Zahlen ≠ 0 der Gleichung
xm − yn = 1,
wobei die Exponenten m und n natürliche Zahlen > 1 sind. Die Vermutung wurde von E. Catalan in einem Brief formuliert und 1844 veröffentlicht, bewiesen wurde sie schließlich 2002 von P. Mihăilescu.
Es gibt eine Reihe von Spezialfällen, die mit relativ elementaren Methoden vor dem endgültigen Beweis behandelt wurden:
| 2n − 3m = 1 | (Levi ben Gershon, ca. 1300) |
| xp − y2 = 1 | (V. Lebesgue, 1850) |
| x2 − y3 = 1 | (L. Euler, 1742). |
1976 erzielte R. Tijdemann ein spektakuläres Resultat, indem er bewies, daß die Catalansche Gleichung nur endlich viele Lösungen hat – die dabei gewonnene Schranke war jedoch viel zu groß für eine Durchmusterung der verbleibenden Kandidaten.
Der Beweis von Mihăailescu verwendet dann ganz andere Methoden, nämlich Resultate aus der Arithmetik der KreisTheilungskörper.
Literatur:
- Catalan, E. (pdf):
- „Note extraite d'une lettre adressée à l'éditeur“
Crelle 27 (1844) - Mihăilescu, P. (pdf):
- „Primary cyclotomic units and a proof of Catalan's conjecture“
Crelle 572 (2004), S. 167-195 - Washington, Lawrence C.:
- „Introduction to Cyclotomic Fields“
Graduate Texts in Mathematics, Vol. 83
Springer-Verlag, New York, 1997
Ergänzende Literatur:
- Bilu, Y. (pdf):
- „Catalan's Conjecture“
Séminaire Bourbaki 909 (2002/2003) - Daems, J. (pdf):
- „A cyclotomic proof of Catalan's conjecture“
Master Thesis, Leiden 2003 - Frey, G.:
- „Der Satz von Preda Mihăilescu: Die Vermutung von Catalan ist richtig!“
DMV-Mitteilungen 4 (2002) - Metsänkylä, T. (pdf):
- „Catalan's Conjecture: Another old Diophantine Problem solved“
Bull. AMS 41 (2004), S. 43-57 - Schoof, René:
- „Catalan's Conjecture“, Reihe: Universitext
Springer-Verlag, New York, November 2008 - Simonson, S. (pdf):
- „The Mathematics of Levi ben Gershon, the Ralbag“
Dpt. of Math and Comp. Sc., Stonehill College, North Easton, MA.
- Neukirch, J. (DOI):
- „Algebraische Zahlentheorie“
Springer-Verlag, New York, 2006 - Samuel, P.:
- „Algebraic Theory of Numbers“
Dover Pub., Dover, 2008
Seminar der WE AlZAGK im SoSe 2008
Mathematische Aspekte der ComputerAlgebra
Do 8:30-10:00 in MZH 7200
(VAK: 03-404)
Ankündigung (als pdf):
In diesem Semester (SS 08) wollen wir uns mit einigen mathematischen Aspekten der ComputerAlgebra beschäftigen. Wir orientieren uns dabei an:
- Cohen, Arjeh M.; Cuypers, Hans; Sterk, Hans (Eds.):
- „Some Tapas of Computer Algebra“
Springer-Verlag, New York, 1999
Die im folgenden angegebenen Kapitel beziehen sich auf dieses Buch.
| Termin | Vortragender | Thema des Vortrages | Literatur | Betreuer |
|---|---|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||||
| 10.04.2008 | -- | Vorbesprechung | ||
| 17.04.2008 | J. Gamst | Überraschung | ||
| 24.04.2008 | M. Dlugosch | Gröbnerbasen, eine Einführung | Kapitel 1 | M. Hortmann |
| 01.05.2008 | -- | Himmelfahrt | ||
| 08.05.2008 | N. Przigoda | Gröbnerbasen und ganzzahliges Programmieren (pdf, Programmcode) | Kapitel 7 | M. Hortmann |
| 15.05.2008 | A. Kankeu | Gröbnerbasen für Codierung | Kapitel 10 | E. Oeljeklaus |
| 22.05.2008 | F. Dreher | Gröbnerbasen für Decodierung (pdf, Programmcode) | Kapitel 11 | E. Oeljeklaus |
| 29.05.2008 | -- | entfällt | ||
| 05.06.2008 | A. Kankeu | Fortsetzung: Gröbnerbasen für Codierung | Kapitel 10 | E. Oeljeklaus |
| 12.06.2008 | B. Walker | Rechnungen in Algebren | Kapitel 5 | J. Gamst |
| 19.06.2008 | S. Schlegel | Endliche Gruppen | Kapitel 8 | J. Gamst |
| 26.06.2008 | A. Scholz | Gitterreduktion | Kapitel 3 | M. Hortmann |
| 03.07.2008 | R. Donau | Faktorisierung von Polynomen | Kapitel 4 | M. Hortmann |
| 10.07.2008 | A. Scholl | Symbolische Polynom-Lösungen | Kapitel 2 | J. Gamst |
Bei dem Buch handelt sich um eine Sammlung von Artikeln und „Projekten“, die aus dem Material zu 2 Minikursen in Eindhoven hervorgegangen sind. Man findet dort Grundlegendes zu GröbnerBasen, GitterReduktion und Polynomfaktorisierung, aber auch Kapitel über:
- Symbolisches Lösen von reellen Polynomgleichungen,
- Symbolisches Lösen von linearen Differentialgleichungen,
- Anwendungen der GröbnerBasen in der Codierungstheorie,
- Anwendungen der GröbnerBasen auf ganzzahliges Programmieren,
- Computeralgebraischer Umgang mit Algebren oder endlichen Gruppen.
Die Themen hängen nur lose miteinander zusammen, die Reihenfolge der Vorträge kann nach den Wünschen der Teilnehmer eingerichtet werden. In jedem Vortrag sollte auch demonstriert werden, wie man die vorgestellten Algorithmen effektiv auf dem Computer einsetzen kann.
Seminar der WE AlZAGK im WiSe 2007/08
Einführung in verschiedene Themenbereiche
Do 8:30-10:00 in MZH 7200
(VAK: 03-404)
Ankündigung (als pdf):
Im WS 07/08 wollen wir Einblicke in 3 ThemenBereiche geben, die für unsere WE von Bedeutung sind: Endliche Körper, CodierungsTheorie, Gröbner Basics. Gedacht ist an jeweils 4-5 Vorträge, in denen relativ leicht zugängliche Tatsachen vorgestellt werden.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||
| 25.10.2007 | -- | Vorbesprechung |
| I. Endliche Körper | ||
| 01.11.2007 | M. Hortmann | Einführung |
| 08.11.2007 | A. Kankeu | Zyklizität der multiplikativen Gruppe und Anzahl der irreduziblen Polynome |
| 15.11.2007 | C. Kapitza | Normalbasen |
| II. Codierungstheorie | ||
| 22.11.2007 | E. Oeljeklaus | Grundbegriffe der Codierungstheorie |
| 29.11.2007 | E. Oeljeklaus | Selbstduale Codes und Gitter |
| 06.12.2007 | S. Yavuz | Gewichtsverteilungen von Codes |
| 13.12.2007 | S. Gessner | Krawtchouk-Polynome |
| 20.12.2007 | S. Gessner | Der Satz von Lloyd |
| Weihnachtsferien | ||
| 10.01.2008 | D. Höffer | Der Satz von Gleason |
| 17.01.2008 | D. Höffer | Der Satz von Gleason (Fortsetzung) |
| III. Gröbnerbasen | ||
| 17.01.2008 | J. Gamst | GröbnerBasics |
| 24.01.2008 | J. Gamst | noch: GröbnerBasics |
| 24.01.2008 | F. Dreher | Elimination und Erweiterung |
| 31.01.2008 | F. Dreher | Elimination und Erweiterung (Fortsetzung) |
- Endliche Körper (M. Hortmann: michaelh@informatik.uni-bremen.de)
- Endliche Körper sind Grundbausteine der Kryptographie und
CodierungsTheorie. Sie entstehen ganz einfach als
Restklassenringe von Z bzgl. einer Primzahl bzw. von F[X] bzgl.
eines irreduziblen Polynoms (wobei F schon ein endlicher Körper
ist) und bieten eine schöne und reichhaltige Theorie.
Behandelt werden können: Struktur der multiplikativen Gruppe, Anzahl und Konstruktion irreduzibler Polynome, Nullstellen und Faktorisierung von Polynomen, Konstruktion und Eigenschaften von Normalbasen.
- CodierungsTheorie (E. Oeljeklaus: oel@math.uni-bremen.de)
- Die CodierungsTheorie beschäftigt sich mit der Entwicklung und
Analyse von Codes, die einen effizienten und verlässlichen
Datentransfer über nicht störungsfreie elektronische
Kanäle ermöglichen. Eine wesentliche Aufgabe der Theorie
besteht darin, Verfahren zu entwickeln, mit denen fehlerhaft
übertragene Daten korrigiert werden können. Die theoretischen
und technischen Möglichkeiten der CodierungsTheorie sind heute
so weit entwickelt, dass z.B. ein guter CD-Player etwa 4000 in
Folge zerstörte Audiobits rekonstruieren kann, ohne dass der
Fehler auf der CD vom menschlichen Ohr wahrnehmbar ist.
Im Seminar wollen wir uns mit einigen interessanten theoretischen Fragestellungen der CodierungsTheorie beschäftigen, deren Lösung im Rahmen eines Seminarvortrages dargestellt werden kann.
- Gröbner Basics (J. Gamst: gamst@math.uni-bremen.de)
- GröbnerBasen sind besonders nützliche Erzeugendensysteme
von Polynomidealen a in K[X1 , . . . , Xn ]. Der Umgang mit ihnen
erfordert den Einsatz von Computern. Sie sind deswegen populär
geworden, weil man mit Hilfe von GröbnerBasen viele Aufgaben
der Idealtheorie algorithmisch lösen kann: Bestimmen von Basen
für Restklassenringe K[X1 , . . . , Xn ]/a, Erzeugung des
Durchschnittes zweier Ideale, Eliminationstheorie.
Im Seminar sollen zunächst die Definition, Charakterisierung und Herstellung von GröbnerBasen behandelt werden, dann vor allem die Anwendung in der Eliminationstheorie.
Seminar der WE AlZAGK im SoSe 2007
Kryptographische Anwendungen elliptischer Kurven
Do 8:30-10:00 in MZH 7200
(VAK: 03-412)
Ankündigung (als pdf):
Im SS 07 werden wir die im letzten Semester erworbenen Kenntnisse benutzen, um zu sehen, wie man elliptische Kurven in der Kryptographie und für zahlentheoretische Algorithmen einsetzen kann. Unsere Grundlage ist weiterhin:
- Washington, L:
- „Elliptic Curves. Number Theory and Cryptography“
Chapman&Hall/CRC, Boca Raton, 2003
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||
| I Kryptographische Anwendungen | ||
| 26.04.2007 | M. Hortmann | Diffie-Hellman-Problem |
| 26.04.2007 | M. Hortmann | Massey-Omura-Verschlüsselung |
| 03.05.2007 | E. Oeljeklaus | ElGamal-Verschlüsselung und -Signatur |
| 10.05.2007 | J. Gamst | RSA mit Elliptischen Kurven |
| 17.05.2006 | -- | Himmelfahrt |
| 24.05.2007 | J. Gamst | Elliptische Kurven mod n |
| II Primzahltests mit Elliptischen Kurven | ||
| 31.05.2007 | A. & G. Grenzebach | Goldwasser-Kilian-Test |
| III Anzahlbestimmung | ||
| 07.06.2007 | M. Albrecht | Baby-Step, Giant-Step |
| 14.06.2007 | S. Lösch | Schoof-Algorithmus |
| 21.06.2006 | -- | Terminplanung |
| IV Faktorisierung mit Elliptischen Kurven | ||
| 28.06.2007 | J. Gamst | Methode von H. Lenstra |
| 05.07.2007 | J. Gamst | Beispiel: Faktorisierung von F10 |
| 12.07.2007 | E. Oeljeklaus | Komplexe Multiplikation und elliptische Kurven |
| 19.07.2007 | M. Hortmann | Komplexe Multiplikation |
Seminar der WE AlZAGK im WiSe 2006/07
Kryptographische Anwendungen elliptischer Kurven
Do 8:30-10:00 in MZH 7200
(VAK: 03-404)
Ankündigung:
Im WS 06/07 werden wir - für eine neue Generation von Studenten - behandeln, wie man mit elliptischen Kurven über endlichen Körpern kryptographisch relevante Algorithmen erhält. Zu Grunde legen wir:
- Washington, L:
- „Elliptic Curves. Number Theory and Cryptography“
Chapman&Hall/CRC, Boca Raton, 2003
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| 26.10.2006 | J. Gamst | Gruppengesetz von elliptischen Kurven |
| 02.11.2006 | A. Grenzebach | Beschreibung elliptischer Kurven |
| 09.11.2006 | G. Grenzebach | Die j-Invariante |
| 16.11.2006 | E. Oeljeklaus | Endomorphismen elliptischer Kurven |
| 23.11.2006 | I. Schäfer | Torsionspunkte |
| 30.11.2006 | T. Nikolayzik | Die WeilPaarung |
| 07.12.2006 | B. Walker | Elliptische Kurven über Fq |
| 14.12.2006 | J. H. Lee | Beweis der Hasse-Abschätzung |
| 21.12.2006 | A. Berthold | Bestimmung der GruppenOrdnung |
| 11.01.2007 18.01.2007 |
R. Donau | Supersinguläre Kurven |
| 25.01.2007 | S. Lösch | Diskrete Logarithmen |
| 01.02.2007 | D. Höffer | Die MOV-Attacke |
| 08.02.2007 | H. Mund | Anomale Kurven |
Seminar der WE AlZAGK im SoSe 2006
Elliptische Funktionen und Modulformen
Do 8:30-10:00 in MZH 7200
(VAK: 03-310)
Ankündigung:
Elliptische Kurven werden klassifiziert durch Punkte der oberen Halbebene H modulo der Aktion der Modulgruppe Γ = SL2(Z). Dabei gilt: der Quotient
Y(Γ) = H / SL2(Z)
trägt die Struktur einer Riemannschen Fläche, und diese kann durch Hinzunahme einer „Spitze“ (die dem Punkt i∞ bei H entspricht) zur Kurve X(Γ), die isomorph zu P1(C) ist, kompaktifiziert werden.
Ähnliche Verhältnisse hat man, wenn man elliptische Kurven mit Zusatzstruktur betrachtet, etwa mit einer ausgewählten zyklischen Untergruppe der Ordnung N. Hierzu gehört auf der oberen Halbebene die Untergruppe
Γ0(N) = { (a,b,c,d) ∈ SL2(Z) : c ≡ 0 mod N }
von Γ, und wenn man erhält durch Kompaktifizieren mit endlich vielen Spitzen aus der Riemannschen Fläche
Y(Γ0(N) ) = H / Γ0(N)
die Modulkurve X(Γ0(N)), welche i.a. nicht einfach zu P1(C) isomorph ist, sondern Geschlecht g ungleich 0 hat.
Nach Konstruktion hat man eine Überlagerungsabbildung
X(Γ0) → X(Γ) = P1(C)
Damit lässt sich das Geschlecht der Modulkurve bestimmen. Der Satz von Riemann-Roch für kompakte Riemannsche Flächen liefert dann Dimensionsformeln für Vektorräume von Modulformen zu Γ0(N).
Gegenstand des Seminars sind diese Zusammenhänge, allgemein für Kongruenzuntergruppen von Γ: nach Definition sollen diese
Γ(N) = Ker ( SL2(Z) → SL2(Z/NZ) )
erhalten.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||
| 20.04.2006 | J. Gamst | Einführung |
| I. Modulformen zu Kongruenzuntergruppen | ||
| 27.04.2006 | J. Gamst | Modulformen zur vollen Modulgruppe |
| 04.05.2006 | J. Siewert | Kongruenzuntergruppen und Modulformen vom Gewicht k |
| 11.05.2006 | A. Grenzebach | Beispiel: Die Eisensteinreihe G2 und das Vierquadrateproblem |
| 18.05.2006 | A. Chabchoub | Komplexe Tori |
| 25.05.2006 | -- | Himmelfahrt |
| 01.06.2006 | G. Grenzebach | Modulräume |
| II. Modulkurven als Riemannsche Flächen | ||
| 08.06.2006 | B. Walker | Hausdorff-Eigenschaft |
| 15.06.2006 | R. Donau | Karten |
| 22.06.2006 | J. Gamst | Elliptische Punkte |
| 29.06.2006 06.07.2006 |
I. Schäfer | Spitzen |
| III. Dimensionsformeln | ||
| 13.07.2006 20.07.2006 |
E. Oeljeklaus | Das Geschlecht der elliptischen Kurve |
| -- | -- | Automorphe Formen und meromorphe Differentiale |
| -- | -- | Dimensionsformeln via Riemann-Roch |
Literatur:
- Diamond, Fred und Jerry Shurman:
- „A first course in modular forms“
Springer-Verlag, New York, 2005 - Freitag, Eberhard und Rolf Busam:
- „Funktionentheorie“
Springer-Verlag, Berlin, 1993 - Koecher, M. und A. Krieg:
- „Elliptische Funktionen und Modulformen“
Springer, Berlin, 1998 - Serre, J.-P.:
- „A course in Arithmetic“
Springer, New York, 1973 - Shimura, G.:
- „Introduction to the Arithmetic Theory of Automorphic Functions“
Princeton University Press, 1971
Seminar der WE AlZAGK im WiSe 2005/06
Elliptische Funktionen und Modulformen
Do 8:30-10:00 in MZH 7200
(VAK: 03-304)
Ankündigung:
Elliptische Funktionen tragen ihren Namen, weil bei der Berechung der Bogenlänge von Ellipsen Integrale der Form
![]()
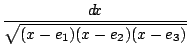
auftreten: deren Umkehrfunktionen geben Anlaß zu doppelt periodischen, meromorphen Funktionen (eben den elliptischen Funktionen), welche der Differentialgleichung (y')2 = (y - e1)(y - e2)(y - e3) genügen und so eine Parametrisierung (y(z), y'(z)) der komplexen Punkte der dann elliptisch genannten Kurve
(E) Y2 = (X - e1)(X - e2) (X - e3)
liefern. Andererseits können die Perioden einer elliptischen Funktion als Gitter
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
mit einem
![]() aus der oberen Halbebene
aus der oberen Halbebene
![]() beschrieben werden, so daß die komplexen Punkte von
(E) auch als Quotient
beschrieben werden, so daß die komplexen Punkte von
(E) auch als Quotient
E![]() =
= ![]() /
/![]()
gewonnen werden können. Nun hat man:
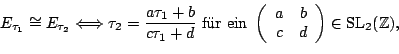
daher sind die elliptischen Kurven klassifiziert durch die elliptische Modulfunktion
j: ![]()
Allgemeiner betrachtet man Quotienten von
![]() nach gewissen Untergruppen von
nach gewissen Untergruppen von
![]() und versteht unter Modulformen Differentialformen auf den zugehörigen
Modulkurven. Hier entsteht eine reichhaltige Welt mit einer Vielzahl von
expliziten Formeln und überraschenden Beziehungen zu Arithmetik und
Geometrie. Das alles findet seinen spektakulärsten Ausdruck im
„Modularity Theorem“ (vormals: Vermutung von Taniyama, Shimura und Weil),
welches 2001 schließlich vollständig bewiesen wurde. Im Seminar
werden wir zunächst die Grundbegriffe im Stil einer
„Funktionentheorie II“ erarbeiten und dann versuchen, eine der Fassungen
des Modularity Theorems zu verstehen.
und versteht unter Modulformen Differentialformen auf den zugehörigen
Modulkurven. Hier entsteht eine reichhaltige Welt mit einer Vielzahl von
expliziten Formeln und überraschenden Beziehungen zu Arithmetik und
Geometrie. Das alles findet seinen spektakulärsten Ausdruck im
„Modularity Theorem“ (vormals: Vermutung von Taniyama, Shimura und Weil),
welches 2001 schließlich vollständig bewiesen wurde. Im Seminar
werden wir zunächst die Grundbegriffe im Stil einer
„Funktionentheorie II“ erarbeiten und dann versuchen, eine der Fassungen
des Modularity Theorems zu verstehen.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||
| 20.10.2005 | J. Gamst | Einführung |
| 27.10.2005 | M. Albrecht, G. Lippold | Die Liouvilleschen Sätze |
| 03.11.2005 | R. Donau | Die Weierstraßsche ℘-Funktion |
| 10.11.2005 | S. Lösch | Der Körper der elliptischen Funktionen |
| 17.11.2005 | I. Schäfer | Das Additionstheorem; die Projektive Ebene über den komplexen Zahlen |
| 24.11.2005 | J. H. Lee | Geometrie des Additionstheorems |
| 01.12.2005 | I. Korobova | Elliptische Integrale |
| 08.12.2005 | T. Nikolayzik | Das Abelsche Theorem |
| 15.12.2005 | J. Gamst | Berechnung des Fagnano-Integrals |
| 12.01.2006 | B. Walker | Die Thetafunktion |
| 19.01.2006 | J. Jaerisch | Die Wärmeleitungsgleichung |
| 26.01.2006 | K. Shaybel | Äquivalenz von Gittern; die Modulfunktion j |
| 02.02.2006 | S. Ebenthal | Der Quotient „obere Halbebene“/PSL(2,Z) |
| 09.02.2006 | N. N. | Meromorphe Modulformen |
Literatur:
- F. Diamond, J.Shurman:
- „A first course in modular forms“
Springer, New York etc., 2005 - R. Busam, E. Freitag:
- „Funktionentheorie“
Springer, Berlin etc., 1993
Seminar der WE AlZAGK im SoSe 2005
InvariantenTheorie
Fr 8:30-10:00 in MZH 7200
(VAK: 03-308)
Ankündigung:
Im SS 05 setzen wir die Beschäftigung mit algorithmischer
Invariantentheorie fort: zunächst für endliche Gruppen, dann
für reduktive Gruppen wie GL(n) oder SL(n).
Vorausgesetzt und benutzt werden nur Kenntnisse über
GröbnerBasen, dazu können die betreffenden Vortragsausarbeitungen
aus dem WS konsultiert werden.
| Invariantenringe endlicher Gruppen | ||
| E1: | Zusammenfassung der im WS behandelten Tatsachen | |
| E2A: | Cohen-Macaulay Eigenschaft: kommutative Algebra | |
| E2B: | Cohen-Macaulay Eigenschaft: Hochster/Eagon und Gegenbeispiel im modularen Fall | |
| E3A: | Invariantenringe von Reflexionsgruppen | |
| E3B: | Kennzeichnung der Reflexionsgruppen. Beispiele | |
| E4: | Noethersche Gradschranke | |
| E5: | Berechnung von GaloisGruppen | |
| E6: | Das Noethersche Problem und generische Polynome | |
| Invariantenringe reduktiver Gruppen | ||
| R1A: | Lineare Algebraische Gruppen | |
| R1B: | Linear reduktive Gruppen: Endlichkeitssatz | |
| R2A: | Derksen Algorithmus: Hauptsatz | |
| R2B: | Derksen Algorithmus: Durchführung und Beispiele | |
| R3: | Spezialfall: Tori | |
| R4: | Spezialfall: GL(n) und SL(n) | |
| R5A: | Berechnung des ReynoldsOperators: CasimirOperator | |
| R5B: | Cayleyscher Omega-Prozeß | |
E5, E6 sind optional und Beginn größerer Projekte.
R4, R5 sind ebenfalls optional: kurze Blicke auf klassische Welten ...
Vortragsausarbeitungen WS 04/05:
- J. Gamst:
- GröbnerBasen und DivisionsAlgorithmus
Raison d'être der Gröbnerbasen - M. Albrecht:
- BuchbergerKriterium
- J. Vogelsang:
- BuchbergerAlgorithmus
- R. Donau:
- Vorbereitungen zur algorithmischen Bestimmung der Hironaka Zerlegung
Literatur:
- D. Cox, J. Little, D. O'Shea:
- „Ideals, Varieties, and Algorithms“
Springer, New York etc., 1992 - D. Benson:
- „Polynomial Invariants of Finite Groups“
Cambridge University Press, 1993 - H. Derksen:
- „Computation of Invariants for Reductive Groups“
Adv. in Math 141 (1999), 366-384 - H. Derksen, G. Kemper:
- „Computational Invariant Theory“
Springer, New York etc., 2002 - K. Geißer, J. Klüners:
- „Galois group computation for rational polynomials“
J. Symb. Comp. 30 (2000), 653-674 - G. Kemper:
- „Computational Invariant Theory“
Queen's Papers in Pure and App. Math. 114 (1998), 5-26 - V. Popov, E. Vinberg:
- „Invariant Theory“
Encyc. of Math. Sciences 55; Springer, New York etc., 1994 - D. Saltman:
- „Groups acting on fields: Noether's problem“
Contemp. Math. 43 (1985), 267-277 - B. Sturmfels:
- „Algorithms in Invariant Theory“
Springer, Wien, 1993.
Seminar der WE AlZAGK im WiSe 2004/05
Algorithmen in der Invariantentheorie
Fr 8:30-10:00 in MZH 7200
(VAK: 03-306)
In diesem Semester befassen wir uns mit Algorithmen in der Invariantentheorie, hauptsächlich nach:
- B. Sturmfels:
- „Algorithms in Invariant Theory“
- D. Cox, J. Little, O. Shea:
- „Ideals, Varieties and Algorithms“
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||
| A. Gröbner Basics | ||
| 29.10.2004 | J. Gamst | Definition und Divisionsalgorithmus |
| 05.11.2004 | M. Albrecht | Buchberger Kriterium |
| 12.11.2004 | J. Vogelsang | Buchberger Algorithmus |
| B. Invarianten endlicher Matrixgruppen | ||
| 19.11.2004 | K. Dikili | Endlichkeitsbeweis |
| 26.11.2004 | C. Grenzebach | Gradschranke |
| 03.12.2004 | M. Hortmann | HilbertReihe |
| 10.12.2004 | E. Oeljeklaus | Noether Normalisierung |
| 17.12.2004 | J. Gamst | Cohen Macaulay Eigenschaft |
| 07.01.2005 | E. Gür | Hironaka Zerlegung |
| C. Algorithmische Bestimmung von Hironaka Zerlegungen | ||
| 14.01.2005 | R. Donau | Teil 1 |
| 21.01.2005 | B. Gohla | Teil 2 |
| 28.01.2005 | I. Schäfer | Teil 3 |
| D. Reflexionsgruppen | ||
| 04.02.2005 | N. N. | Struktur des Invariantenrings |
| 11.02.2005 | N. N. | Kennzeichnung der Reflexionsgruppen |
Seminar der WE AlZAGK im SoSe 2004
Algebraische Kurven
Di 8:30-10:00 in MZH 7200
(VAK: 03-304)
Im SoSe 04 wollen wir uns die Theorie Algebraischer Kurven, insbesondere über einem endlichen Grundkörper, aneignen. Dabei haben wir uns festgelegt auf das Lehrbuch
- W. Lütkebohmert:
- „Codierungstheorie“, Vieweg 2003
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||
| 27.04.2004 | M. Hortmann | Hilbertscher Nullstellensatz (nach D.Eisenbud: „Commutative Algebra“, I.1.6) |
| 04.05.2004 | I. Meyer | Algebraische Kurven (Lüt 6.1.1, 6.1.2) |
| 11.05.2004 | J. Gamst | Bericht und Ausblick (Lüt 6.1 Rest) |
| 18.05.2004 | J. Vogelsang | Ebene Kurven (Lüt 8.1.1) |
| 25.05.2004 | S. Utecht | Ganze RingErweiterungen (Lüt A.3) |
| 01.06.2004 | A. Chabchoub | Differentiale (Lüt A.3) |
| 08.06.2004 | R. Donau | Multiplizität (Lüt 8.1.2) |
| 15.06.2004 | M. Albrecht | Schnittzahl (Lüt 8.1.3) |
| 22.06.2004 | E. Oeljeklaus | Desingularisierung: Aufblasungen (Lüt 8.2.1) |
| 29.06.2004 | J. Gamst | Desingularisierung: Cremona Transfomationen (Lüt 8.2.2) |
| 06.07.2004 | N. N. | Satz von Riemann-Roch (Lüt 8.3) |
| 13.07.2004 | N. N. | Residuensatz (Lüt 8.4) Hurwitzsche Geschlechterformel (Lüt 8.5) |
Bei der Multiplizität und der Schnittzahl sowie der Desingularisierung bietet es sich auch an, das ComputerSystem SINGULAR kennenzulernen. Das wird am besten in begleitenden Übungen geschehen.
Seminar der WE AlZAGK im WiSe 2003/04
Kryptoanalyse
Di 8:30-10:00 in MZH 7200
(VAK: 03-302)
Wir beginnen mit drei Vorträgen über Torische Codes, zu denen wir im Sommersemester nicht mehr gekommen sind:
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| 14.10.2003 | I. Bergen | Fehlerkorrigierende Codes |
| 21.10.2003 | I. Bergen | Hansen Codes |
| 28.10.2003 | I. Bergen | Schranken bei Hansen Codes |
Dabei werden die im Sommersemester erworbenen Kenntnisse über Torische Varietäten vertieft und auf den Fall eines endlichen Grundköpers übertragen.
Ab November wenden wir uns dann einem neuen Thema zu: Kryptoanalyse. Hier interessiert uns zunächst die Analyse der Hashfunktion MD4 durch H. Dobbertin, vgl.
- H. Dobbertin:
- „Cryptanalysis of MD4“
Lecture Notes of Comp. Sc. 1039, p. 53-59. - H. Dobbertin:
- „Cryptanalysis of MD4“
J. of Cryptology 11 (1998), p. 253-271
Anschließend möchten wir uns algebraischen Strukturen zuwenden, die bei der Analyse moderner Blockchiffrieralgorithmen entdeckt wurden. Insbesondere würde die Lösbarkeit großer quadratischer Gleichungssysteme den neuen Standard AES entscheidend schwächen.
- S. Murphy, M. J. B. Robshaw:
- „Essential Algebraic Struktures within the AES“
Lect. Notes of Comp. Sc. 2442, p. 1-16.
Literatur findet man auch hier.
Seminar der WE AlZAGK im SoSe 2003
Torische Varietäten und torische Codes
Di 8:30-10:00 in MZH 7200
(VAK: 03-302)
In diesem Semester beschäftigen wir uns mit torischen Varietäten und torischen Codes über endlichen Körpern. Hierzu orientieren wir uns an:
- D. A. Cox:
- „Tutorial on Toric Varieties“
Workshop on Alg. Geometry and Geom. Modeling, Vilnius, July 30th 2002. - D. Joyner:
- „Toric Codes over Finite Fields“
Preprint, 21.August 2002. - L. Kaup:
- „Vorlesungen über Torische Varietäten“
Konstanzer Schriften in Math. und Inf. (130), Oktober 2000.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| 29.04.2003 | J. Gamst | Einführung |
| 06.05.2003 | R. von Rahden | Konvexe polyedrische Kegel |
| 13.05.2003 | I. Bergen | Affine torische Varietäten |
| 20.05.2003 | M. Hortmann | Normalität |
| 27.05.2003 | I. Meyer | Fächer und torische Varietäten |
| 03.06.2003 | E. Oeljeklaus | Kompaktheit und Glattheit |
| 10.06.2003 | Divisoren auf torischen Varietäten | |
| 17.06.2003 | Geradenbündel auf torischen Varietäten | |
| 24.06.2003 | Dimensionsformel | |
| 01.07.2003 | Fehlerkorrigierende Codes | |
| 08.07.2003 | Hansen Codes | |
| 15.07.2003 | Schranken bei Hansen Codes |
Bei den Vorträgen am 10./17./24. Juni müssen wir die Standard-Literatur zu Hilfe nehmen:
- W. Fulton:
- „Introduction to Toric Varieties“
Annals of Math.Studies (131), Princeton Univ. Press 1993. - T. Oda:
- „Convex Bodies and Algebraic Geometry“
Erg. der Math.(15), Springer 1985.
Seminar der WE AlZAGK im WiSe 2002/03
Primzahlen und Faktorisierung ganzer Zahlen
Di 10:00-12:00 in MZH 7200
(VAK: 03-302)
Ankündigung:
Primzahlen und Faktorisierung ganzer Zahlen - das sind zwei der ältesten Themen in der Mathematik. Nach dem Vorbild von D. Knuth ist es üblich, hier Gauß zu zitieren:
Problema, numeros primos a compositis dignoscendi, hosque in factores suos primos resolvendi, ad gravissima ac utilissima totius arithmeticae pertinere, et geometrarum tum veterum tum recentiorum industriam ac sagacitatem occupavisse, tam notum est, ut de hac re copiose loqui superfluum foret.
Dass die Aufgabe, die Primzahlen von den zusammengesetzten zu unterscheiden und letztere in ihre Primfactoren zu zerlegen, zu den wichtigsten und nützlichsten der gesamten Arithmetik gehört und die Bemühungen und den Scharfsinn sowohl der alten wie auch der neueren Geometer in Anspruch genommen hat, ist so bekannt, dass es überflüssig wäre, hierüber viele Worte zu verlieren.
(Artikel 329 in den Disquisitiones Arithmeticae).
Im Zeitalter der Computer haben diese Fragen eine neue Dringlichkeit erhalten: für kryptographische Zwecke werden große Primzahlen benötigt, und die Sicherheit des RSA-Verfahrens beruht darauf, daß die Faktorisierung großer Zahlen einen Aufwand erfordert, den die gegenwärtigen Hilfsmittel nicht leisten können.
Schon der Nachweis, daß eine Zahl mit etwa 500 Dezimalstellen eine Primzahl ist, führt auf nichttriviale Probleme, bei denen es immer wieder neue Entwicklungen gibt, so zuletzt durch eine Gruppe indischer Wissenschaftler:
- M. Agrawal, N. Kayal, N. Saxena:
- „Primes is in P“
6. Aug. 2002.
Im WS wollen wir eine Einführung in den Themenkreis geben, bei der zunächst noch keine besonderen Vorkenntnisse vorausgesetzt werden.
- Primzahltests nach Lucas, Proth und Pocklington, insbesondere für Mersenne- und Fermatzahlen, aber auch das neue Verfahren aus Indien.
- Faktorisierung bei den Pionieren im 19. Jahrhundert, bis hin zur Kettenbruchmethode von Brillhart und Morrison 1975.
Funktionentheoretische Hilfsmittel werden benötigt, um Methoden zur Nullstellenbestimmung bei der Riemannschen ZetaFunktion zu verstehen - dabei wollen wir auch die Bedeutung der Riemannschen Vermutung für die Beschreibung der Primzahlverteilung diskutieren.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | ||
| 22.10.2002 | I. Bergen | Solving Pell`s Equation |
| 29.10.2002 | J. Gamst | Primzahltests nach E. Lucas |
| 05.11.2002 | L. Mozgovenko | Mersenne Zahlen |
| 12.11.2002 | O. Michel | Fermat Zahlen |
| 19.11.2002 | P. H. Taffou | Primzahltests nach F.Proth und H.C Pocklington |
| 26.11.2002 | D. Dahme/ D. Lubert | Der indische Primzahltest |
| 03.12.2002 | M. Albrecht/D. Best | Faktorisierung nach T. Pépin und P. Seelhoff |
| 10.12.2002 | Ch. Ober-Blöbaum | Die Faktorisierung von M67 |
| 17.12.2002 | T. Rompf/ J. Schuller | Der Algorithmus von M. A. Morrison und J. Brillhart |
| 07.01.2003 | Riemannsche Zeta-Funktion | |
| 14.01.2003 | I. Meyer | Funktionalgleichung |
| 21.01.2003 | S. Mittwollen | Bedeutung für die Beschreibung der Primzahlverteilung |
| 28.01.2003 | L. Fischer | Berechnung der Nullstellen nach Gram |
| 04.02.2003 | Berechnung der Nullstellen nach R. Brent | |
Literatur:
- E. Bombieri:
- „Problems of the Millennium: The Riemann Hypothesis“
Publ. of the Clay Institute. - R. Crandall, C. Pomerance:
- „Prime Numbers. A Computational Perspective“
Springer-Verlag 2001. - M. Morrison, J. Brillhart:
- „A method of factoring and the factorization of F7“
Math. of Comp. (29), 1975. - G. Nebe:
- „Faktorisieren ganzer Zahlen“
Jahresb. DMV (102) 2000. - A. Odlyzko:
- „Analytic Computations in Number Theory“
in Proc. Symp. Appl. Math. (48) 1994. - H. C. Williams, J. O. Shallit:
- „Factoring Integers before Computers“
in Proc. Symp. Appl. Math. (48) 1994.
Seminar der WE AlZAGK im SoSe 2002
Algorithmische Zahlentheorie
Di 8:30-10:00 in MZH 6115
(VAK: 03-303)
In diesem Semester setzen wir die Beschäftigung mit der algorithmischen Zahlentheorie fort, weiterhin im wesentlichen nach
- H. Cohen:
- „A Course in Computational Algebraic Numer Theory“
Springer 1993.
| Programm: | |
|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | |
| I. | Polynomfaktorisierung über Z mit GitterbasisReduktion |
| (3 Vorträge nach A. K. Lenstra, H. W. Lenstra, L. Lovász: „Factoring Polynomials with Rational Coefficients“. Math. Ann. 261, 515-534 (1982)). Jens Gamst, Lutz Fischer | |
| II. | Darstellung von Moduln und Idealen |
| (3 Vorträge nach Cohen 4.7, 6.1.3) Eberhard Oeljeklaus, Ingolf Meyer | |
| III. | Zerlegung von Primzahlen: p teilt/teilt nicht [O : Z[θ]] |
| (3 Vorträge nach Cohen 4.8, 6.2) Ralf Stein, N.N. | |
| IV. | Berechnung von Klassengruppen und FundamentalEinheiten |
| (nach Cohen 6.5) Michael Hortmann, N.N. | |
| V. | Lösung der Pellschen Gleichung |
| (nach H. W. Lenstra: „Solving the PellEquation“, Notices AMS, Feb.2002) Ina Bergen, Claas Grenzebach (pdf, ps) | |
Aus dem Wintersemester benutzen wir, neben dem Weltbild der Algebraischen Zahlentheorie, die Grundtatsachen über Hermitesche Normalformen, GitterbasisReduktion und Bestimmung der maximalen Ordnung nach Zassenhaus.
Seminar der WE AlZAGK im WiSe 2001/02
Algorithmische Zahlentheorie
Di 8:30-10:00 in MZH 6115
(VAK: 03-302)
In den letzten Jahrzehnten hat es große Fortschritte bei der algorithmischen Behandlung von Fragen der Zahlentheorie gegeben, von der Faktorisierung von Polynomen mit ganzzahligen Koeffizienten über die Bestimmung der maximalen Ordnung in Zahlkörpern bis zu erstaunlich expliziten Berechnungen in der Klassenkörpertheorie. Die Bibel hierfür sind die beiden Werke von H. Cohen:
- H. Cohen:
- „A Course in Computational Algebraic Numer Theory“
Springer 1993. - H. Cohen:
- „Advanced Topics in Computational Number Theory“
Springer 2000.
Im kommenden Semester werden wir zunächst ausgewählte Themen aus dem ersten der beiden Bücher behandeln.
| Programm: | |
|---|---|
| I. | Lineare Algebra über Z |
| Hermitesche und Smithsche Normalform | |
| (2 Vorträge nach Cohen 2.4) | |
| II. | Gitterreduktion nach A. K. Lenstra, H. W. Lenstra, L. Lovász |
| (3 Vorträge nach Cohen 2.5) | |
| III. | Faktorisierung von Polynomen über Fp und über Z |
| (3 Vorträge nach Cohen 3.3-3.5) | |
| IV. | Algorithmen für Zahlkörper |
| 1. Das Unterkörperproblem (Cohen 4.5) | |
| 2. Darstellung von Idealen (Cohen 4.7) | |
| 3. Klassenzahl imaginärquadratischer Zahlkörper (Cohen 5.3.2) | |
| 4. Berechnung der maximalen Ordnung (Cohen 6.1) | |
| V. | Zerlegung von Primzahlen |
| (3 Vorträge nach Cohen 6.2) | |
Seminar der WE AlZAGK im SoSe 2001
QuantenComputerAlgorithmen
Di 8:30-10:00 in MZH 6115
(VAK: 03-311)
Seit den achtziger Jahren des vorigen Jahrhunderts wird diskutiert, ob man
nicht Computer kontruieren könne, deren Arbeitsweise auf
quantenmechanischen Prinzipien beruht: eben QuantenComputer.
Ihre Dringlichkeit erhielt die Frage, als P. Shor 1994 einen Algorithmus
vorstellte, mit dem auf einem QuantenComputer ganze Zahlen in polynomialer
Zeit in Faktoren zerlegt werden können -- damit wäre ein
großer Teil der Verfahren in der public-key-Kryptographie
hinfällig.
Wir legen zu Grunde:
- A. O. Pittenger:
- „An Introduction to Quantum Computing Algorithms“
Birkhäuser, Bosten etc, 2000. - J. Preskill:
- „Quantum Computation“
Lecture Notes for Physics 219/Computer Science 219 at Caltech,
http://www.theory.caltech.edu/people/preskill/ph219/
und zusätzlich Artikel (s.u.)
| Programm: | |
|---|---|
| Eine Übersicht der Vortragsausarbeitungen findet sich hier. | |
| I. Quantenmechanische Grundlagen | |
| Allgemeinheiten, Qubits, Spekulation über Realisierungen (2 Vorträge) | |
| 10.04.2001 | Lüder Basedow |
| 17.04.2001 | Ina Bergen |
| II. Operationen auf QuantenComputern | |
| Quantum Gates, Arithmetik, endliche FourierTransformation (3 Vorträge) | |
| 24.04.2001 | Ingolf Meyer |
| 08.05.2001 | Claas Grenzebach (pdf, ps) |
| 15.05.2001 | Jens Gamst |
| III. Quantenalgorithmen | |
| Algorithmen von Deutsch und Simon, Suchalgorithmus von Grover, Faktorisierungsalgorithmus von Shor (6 Vorträge) | |
| Marc Suling (pdf, ps), Christoph Schubert, Dirk Stadil, Jörg Trommer | |
| IV. QuantenCodes | |
Hier gibt es ein wenig Literatur (postscript) zum herunterladen:
- H. E. Brandt: „Quantum Devices“
- D. Gottesmann: „An Introduction to Quantum Error Correction“
- S. J. Lomonaco: „A Rosetta Stone for Quantum Mechanics and an Introduction to Quantum Computation“
- J. Preskill: „Quantum Computation“, Chapter 1-6, Chapter 7
- J. Preskill: „Quantum Computing: Pro and Con“
- P. Shor: „Introduction to Quantum Algorithms“
- U. Vazirani: „Quantum Complexity Theory“
Eine Liste dieser und weiterer Artikel findet man auf der Seite:
http://www.theory.caltech.edu/people/preskill/ph219/
Eine Liste von Quanten Computer Simulatoren gibt es auf der Seite:
http://www.dcs.ex.ac.uk/~jwallace/simtable.htm
Außerdem noch eine Liste einiger Artikel, die man sich bei „Physikal Review Online Archive“ als PDF-Dokument herunterladen kann (der link führt zunächst zu einem abstract des entsprechenden Artikels):
- V. Vedral, A. Barenco and A. Ekert: „Quantum networks for elementary arithmetic operations“
- R. B. Griffiths and C. Niu: „Semiclassical Fourier Transform for Quantum Computation“
- A. Ekert and R. Jozsa: „Quantum computation and Shor's factoring algorithm“
Seminar der WE AlZAGK im WiSe 2000/01
Kryptographisch relevante Algorithmen für elliptische Kurven
Fr 8:00-10:00 ct in MZH 6115
(VAK: 03-300)
In diesem Semester führen wir das Studium kryptographisch relevanter Algorithmen für elliptische Kurven fort, dabei geht es vor allem um den Schoof-Algorithmus zur Berechnung der GruppenOrdnung. Es wird weiterhin zu Grunde gelegt:
- I. Blake et al.:
- „Elliptic Curves in Cryptography“
Cambridge Univ. Press 1999.
und zusätzlich der Überblicksartikel
- R. Schoof:
- „Counting Points on Elliptic Curves over Finite Fields“
J. Th. des Nombres Bordeaux 7, 219-254, 1995.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| Kryptographisch schwache Kurven | ||
| 20.10.2000 | Jens Gamst | Supersinguläre und anomale Kurven |
| 27.10.2000 | Jens Gamst | Elliptische Kurven über Qp |
| 03.11.2000 | Jens Gamst | p-adischer elliptischer Logrithmus |
| Berechnung der GruppenOrdnung | ||
| 10.11.2000 | Sven Ehlers | Shanks-Mestre Algorithmus |
| 17.11.2000 | Ralf Stein | Schoof-Algorithmus: Überblick |
| 24.11.2000 | Eberhard Oeljeklaus | Benutzung der ZetaFunktion |
| Die Ideen von Atkin und Elkies | ||
| 01.12.2000 | Gregor Leander | Elkies- und Atkin-Primzahlen |
| 08.12.2000 | Jens Gamst | Allgemeinheiten über modulare Polynome |
| 15.12.2000 | Jens Gamst | Lemma von Lercier/Schoof |
| 22.12.2000 | Eberhard Oeljeklaus | Isogenien vom Grad l |
| Faktoren von Divisionspolynomen (ungerade Charakteristik) | ||
| 12.01.2001 | Komplexe Modelle | |
| 19.01.2001 | Rechnung mit klassischen modularen Polynomen | |
| 26.01.2001 | Bestimmung der Spur des Frobenius mod l | |
| 02.02.2001 | Finale: Spur des Frobenius | |
| 09.02.2001 | Beispiele | |
Seminar der WE AlZAGK im SoSe 2000
Kryptographisch relevante Algorithmen für elliptische Kurven
Fr 8:00-10:00 ct in MZH 6115
(VAK: 03-431)
In diesem Semester geht es um kryptographisch relevante Algorithmen für elliptische Kurven. Grundlegende Resultate wie die Hasse-Abschätzung werden wir einfach zur Kenntnis nehmen, um dann vor allem den Schoof-Algorithmus zur Berechnung der GruppenOrdnung zu studieren. Die zu Grunde gelegte Literatur:
- I. Blake et al.:
- „Elliptic Curves in Cryptography“
Cambridge Univ. Press 1999.
Es reichen Vorkenntnisse in Algebra im Umfang der Veranstaltungen zum Vordiplom.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| 14.04.2000 | Jens Gamst | Additionsgesetz |
| 28.04.2000 | Ralf Stein | Elliptische Kurven über endlichen Körpern |
| 05.05.2000 | Sven Ehlers | Divisionspolynome |
| 12.05.2000 | Eberhard Oeljeklaus | Weil-Paarung und Isogenien - Einführung |
| 19.05.2000 | Eberhard Oeljeklaus | Weil-Paarung und Isogenien - Teil 2 |
| 26.05.2000 | Anne Witt | Die Methoden von Shanks und Pollard |
| 02.06.2000 | Jens Gamst | Isogenien über C. |
| 09.06.2000 | Jens Gamst | H1 und Kummer |
| 23.06.2000 | Gregor Leander | MOV-Attacke, Teil 1 |
| 30.06.2000 | Gregor Leander | MOV-Attacke, Teil 2 |
Seminar der WE AlZAGK im WiSe 1999/2000
Codierungstheorie
Fr 8:00-10:00 ct in MZH 6115
(VAK: 03-449)
In diesem Semester befassen wir uns mit Codierungstheorie, zunächst an Hand des Buches:
- J.H. van Lint:
- „Introduction to Coding Theory“
Springer 1989.
Es reichen Vorkenntnisse in Stochastik und Algebra im Umfang der Veranstaltungen zum Vordiplom.
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| 22.10.1999 | Jens Gamst | Einführung |
| 29.10.1999 | Eberhard Oeljeklaus | Ein Satz von Shannon, Teil 1 |
| 05.11.1999 | Eberhard Oeljeklaus | Ein Satz von Shannon, Teil 2 |
| 12.11.1999 | Sven Ehlers | Fehlerkorrigierende lineare Codes |
| 19.11.1999 | Gregor Leander | Binärer und ternärer GolayCode |
| 26.11.1999 | Ralf Stein | Reed-Muller Codes |
| 03.12.1999 | Ralf Stein | Majority Logic Decoding |
| 10.12.1999 | Anne Witt | Untere und obere Schranken für Codes I |
| 17.12.1999 | Anne Witt | Untere und obere Schranken für Codes II |
| 14.01.2000 | Carsten Kohley | Goppa Codes |
| 21.01.2000 | Jens Gamst | Algebraic Geometry Codes - Überblick |
| 28.01.2000 | Eberhard Oeljeklaus | Zyklische Codes |
| 04.02.2000 | BCH-Codes | |
| 11.02.2000 | Michael Hortmann | Reed-Solomon Codes |
Seminar der WE AlZAGK im SoSe 1999
Grundlagen der Kryptologie
Fr 8:00-10:00 ct in MZH 6115
(VAK: 03-449)
In diesem Semester befassen wir uns mit Grundlagen der Kryptologie:
| Termin | Vortragender | Thema des Vortrages |
|---|---|---|
| 16.04.1999 | Wenke Sietas | Kryptographische Hashfunktionen - Teil 1 |
| 23.04.1999 | Sönke Maseberg | Kryptographische Hashfunktionen - Teil 2 |
| 30.04.1999 | Gregor Leander | Data Encryption Standard (DES) - Teil 1 |
| 07.05.1999 | Tim Schneider | Data Encryption Standard (DES) - Teil 2 |
| 14.05.1999 | Franziska Hennig | Zero-Knowledge Verfahren - Teil 1 |
| 21.05.1999 | Jens Gamst | Zero-Knowledge Verfahren - Teil 2 |
| 04.06.1999 | Ralf Stein | Quantencomputer |
| 11.06.1999 | Sven Ehlers | Quantenkryptographie |
| 18.06.1999 | Axel Pieke | Statistische Eigenschaften von Texten, Entropie nach Shannon |
| 25.06.1999 | Protokolle - Teil 1 | |
| 02.07.1999 | Protokolle - Teil 2 |